SOLDAGEM POR EXPLOSÃO
A soldadura por explosão ocorre sem fusão na interface, assim não há problemas metalúrgicos associados a este tipo de soldadura (mesmo que ocorra alguma fusão pontual, não surgem problemas, pois o processo é feito a uma pressão muito elevada e num espaço de tempo muito reduzido – na ordem dos s).
Mecanismo da soldadura por explosão
Este mecanismo consiste na projecção de um determinado material (chapa voadora) sobre outro (chapa base), ou de um contra o outro. Este pode ser utilizado no capeamento de metais, soldadura dos tubos aos espelhos em permutadores de calor, ligar peças em Cu a Al para condução de electricidade, etc. Considerando o capeamento de materiais (fig. 2.1), teremos uma chapa voadora que sob a acção de uma onda de detonação de um explosivo é projectada contra uma chapa base a uma alta velocidade. Como a pressão originada no ponto de colisão é bastante elevada, a resistência ao corte dos materiais em questão é praticamente desprezável em função daquele valor, e a tensão de corte dos dois componentes metálicos é altamente excedida (no ponto de colisão são entre 10-60). Os materiais têm um comportamento na vizinhança do ponto de colisão como fluidos não miscíveis – teoria de Crossland e Bahrani.
Fig. 2.1
Esquema de capeamento de metais.
Geometria do sistema
Neste processo de soldadura, existem dois tipos de preparação importantes:
- Geometria paralela (fig. 2.2a)
- Geometria angular (fig. 2.2b)
Fig. 2.2
O primeiro tipo de preparação consiste na disposição inicial angular entre as matérias e o segundo numa disposição paralela entre os materiais a soldar. A geometria angular permite uma maior liberdade de escolha do explosivo, pois o explosivo pode ter uma
velocidade de detonação maior do que a velocidade do som nos metais que pretendemos soldar, mas com a inclinação, a velocidade de soldadura pode ser inferior.
Parâmetros da soldadura por explosão
Para o processo de soldadura necessitamos de controlar muitos parâmetros.
O processo de soldadura é dividido basicamente em três estádios:
- a detonação de cargas explosivas,
- a deformação e aceleração da chapa voadora ou componentes,
- a colisão entre os componentes a soldar.
A detonação da carga explosiva promove a energia necessária para a deformação e aceleração do elemento voador, para que este transponha a distância entre ambos os elementos a soldar e se unam.
Durante a colisão entre os componentes a soldar ,o elemento voador adquire uma quantidade de movimento e uma velocidade Vp no ponto de colisão com o componente estacionário, onde a energia cinética é dissipada ocorrendo a soldadura entre os componentes.
No caso de colisões múltiplas, bem como na soldadura de estruturas com várias camadas, o processo é repetido para cada interface ( Fig. 2.3 ). A energia cinética é reduzida em cada interface quando o impacto interlaminar ocorre obrigando ao progressivo aumento da massa acelerada. Nalguns casos é usado um sistema adicional para proteger a superfície de cima de produtos da detonação (buffer) e, se necessário, uma placa direccional para aumentar artificialmente a massa e, por conseguinte, a quantidade de movimento dos componentes acelerados.
Fig.2.3
Os parâmetros de soldadura que influenciam ambas as condições finais na região da colisão e o modo como a energia é dissipada variam ,em termos gerais, com: a velocidade de impacto Vp, a velocidade no ponto de colisão Vc e o ângulo dinâmico de colisão .
O valor destes parâmetros pode variar através da alteração da geometria do sistema, do tipo de carga, da velocidade de detonação, da chapa direccional, do sistema de resguardo contra produtos de detonação e da distância entre os componentes a soldar. A geometria pode ser com a chapa voadora em posição paralela ou oblíqua. Os parâmetros acima mencionados podem ser calculados facilmente considerando em pormenor a mecânica da transferência da quantidade de movimento da carga para a placa voadora, a continuidade do fluxo através da região de colisão em coordenadas transformadas e a deformação dinâmica da chapa .
Parâmetros de colisão
Diferentes autores têm apontado diferentes direcções acerca da velocidade da placa voadora e, consequentemente, das relações entre as diferentes velocidades obtidas a partir dos diagramas de velocidade, concluindo-se que diferem em cada caso. Na figura 2.4 a), assume-se que Vp divide em dois iguais, o ângulo entre a porção da chapa já acelerada, atrás da frente de detonação e da porção não deformada. Esta suposição foi justificada por Birkhoff, para o caso duma superfície cónica axissimétrica considerando a continuidade do fluxo de massa através do ponto de colisão. A figura 2.4 b), implica que Vp é perpendicular à chapa depois da detonação, o que significa que as partes aceleradas rodam segundo o eixo de rotação plástica, formado na frente de detonação, enquanto o triângulo equilátero na figura 2.4 c) dá Vc=Vf, isto é, o comprimento da chapa voadora permanece inalterado. Na figura 2.4 d), Vp é perpendicular a uma linha bissectora do ângulo inicial e na figura 2.4 e), Vp é perpendicular à chapa na sua posição inicial.
Fig. 2.4
Diagramas de velocidade, (a-d) configuração proposta por vários autores, (e) diagrama baseado em Vp normal em relação à posição original.
Comparando as respectivas configurações, vê-se que o ângulo , que define a direcção Vp, difere nos cinco casos, dando,
B>A>C>D (2.1)
para o caso mostrado na figura 2.4 b) e com referência à figura 2.4 e) as seguintes relações podem ser deduzidas:
VP=Dsin(-)
Vf=DPcot (2.2)
Vc=VPsin
=sin-1(VP/Vc)=+
Relações similares podem ser facilmente obtidas para outras configurações. Várias fórmulas empíricas e semi-empíricas para a previsão de Vp têm sido sugeridas e resultados experimentais indicam uma boa concordância com os valores previstos. A equação de Gurney, introduzida na Segunda Guerra Mundial, dá a velocidade da chapa como uma função da energia de explosão e da razão entre a carga e a massa da chapa. Para uma detonação unidimensional:
(2.3)
A equação foi examinada mais tarde por Stern que sugeriu uma alternativa ligeiramente diferente:
(2.4)
onde Ek é a energia cinética de explosão,
, em que é a massa da carga por unidade de área e a massa da placa por unidade de área.
Deribas obteve dados experimentais para velocidades de detonação baixas, explosivos granulares e obteve a seguinte equação:
(2.5)
Da dinâmica dos gases obteve a seguinte expressão:
(2.6)
Onde D é a velocidade de detonação.
As equações 2.3 e 2.6 são baseadas na detonação unidimensional (num plano perpendicular a este sobre o componente voador e paralelo a D). Uma solução bidimensional aproximada foi obtida por Duval e Erkman, multiplicando a velocidade Vp de 2.3 por um factor de , onde
(2.7)
e VG é a velocidade das partículas dos gases de detonação atrás da frente de detonação.
A precisão do factor de ajustamento diminui à medida que o comportamento do material explosivo deixa de ser ideal. A tabela 2.1, sumaria valores típicos de EK, E0 e . Uma correcção similar foi executada por Takizawa. Isto conta para o desvio da velocidade de detonação a partir do seu valor ideal, e é dado por:
(2.8)
onde Vp é a velocidade da chapa em, m/s, te a espessura do explosivo em mm, D é a velocidade de detonação da carga de espessura te, D0 a velocidade de detonação ideal numa carga de espessura infinita, E0 a energia disponível da expansão adiabática dos gases da explosão e R a razão entre a carga e a chapa.
tabela 2.1
Constantes de explosivos para uso da equação de Gurney modificada.
Condições limites para soldadura
Resultados experimentais indicam que há valores críticos tanto para os parâmetros de colisão como para os geométricos que têm de ser observados. Assim, os parâmetros excedidos ou não, dependem do sistema, de modo a obter uma soldadura aceitável, parâmetros esses que se resumem de seguida:
(1) Como é necessário um jacto na região de colisão, deve ser excedido um ângulo mínimo de colisão, . Para cada metal o valor desse ângulo é função da velocidade de colisão.
(2) A velocidade de colisão, Vc, e a velocidade da placa, Vp, deve ser menor que a velocidade do som em ambos os componentes de soldadura. Esta condição foi estabelecida experimentalmente por El-Sobky e Blazynski como uma explicação de condição necessária para a tensão das ondas reflectidas não interferir na onda de incidência no ponto de colisão. Também é sabido que a velocidades supersónicas a pressão dinâmica não é mantida por um período suficientemente longo para que se criem condições físicas para os ajustamentos de difusão interatómica e de equilíbrio na região de colisão. Embora Wylie tenha sugerido que a velocidade do som possa ser excedida até 25%, a colisão subsónica parece ser mais satisfatória. Como Vc está relacionado com D e , pode ser ajustado, reduzindo a velocidade de detonação ou introduzindo um ângulo inicial oblíquo a velocidade do som, ou mais concretamente, a velocidade de propagação da onda de tensão limita superiormente Vp e Vc.
(3) Uma pressão mínima de impacto deve ser excedida (e daí também a velocidade Vp), de modo que a energia de impacto seja suficiente para proceder à soldadura. Sugere-se que a energia de impacto requerida esteja relacionada com a energia de tensão e a energia dinâmica de deformação do material voador. Um limite superior de energia é também requerido para prevenir o aquecimento, evitando fusão por dissipação viscosa e formação de camadas frágeis.
(4) Uma distância suficiente, S, deve ser providenciada de modo a que o componente voador possa ser acelerado para a velocidade requerida. Consideram-se valores satisfatórios os que variam entre 0.5 e1.0 vezes a espessura da chapa voadora. São apontados, por Ezra, diferentes valores de distância entre placas a soldar, os quais dependem da massa específica do material voador. Estes são múltiplos da espessura (1/2-2/3), (1/2-1), (2/3-2) para massas específicas com menos de 5, entre 5-10 e maiores que 10, respectivamente.
Do sumário dos parâmetros importantes acima citados, podemos concluir que a interacção entre os parâmetros de geometria dinâmica de colisão, por um lado, e as características do material, por outro, tornam difícil a separação dos respectivos esforços. Consequentemente, alguns autores tentam estimar a energia total requerida e com isto calcular a carga de explosivo, de preferência com base em aproximações teóricas da mecânica do processo. Blazynski e Dara, por exemplo, usaram a análise dimensional para deduzir a seguinte e relevante equação, respeitante à soldadura de cilindros duplos
(em unidades S.I.) (2.9)
Onde E é a energia de explosão, a densidade do material voador, L o comprimento da ligação, t a espessura da chapa voadora, d a espessura do cilindro voador e D a velocidade de detonação.
Usando o mesmo método, Kowalick e Hay obtiveram para o componente plano:
(2.10)
K é uma constante, R a carga a aplicar, c a velocidade do som no material voador e t a sua espessura. Cada uma destas duas relações, 2.9 e 2.10, é essencialmente uma aproximação, desde que não se consiga estabelecer a correlação entre os grupos de menor dimensão. Carpenter deduziu outra expressão, baseada no balanço, entre a energia de explosão e a soma da energia cinética e da energia elasto - plástica de deformação da placa voadora, sendo esta da seguinte forma:
(2.11)
onde o sufixo e denota material explosivo e Y a tensão de cedência, S a distância entre a chapa base e a chapa voadora, o ângulo inicial, , o angulo dinâmico de colisão.
As expressões acima mencionadas, embora não exactas, conduzem a um razoável grau de sucesso e podem ser usadas juntas em experiências acumuladas, de modo a produzir a informação necessária. Contudo, a existência de um largo número de parâmetros e as suas interdependências obrigam a idealizar um método mais sistemático de classificação funcional dos parâmetros básicos. Christensen, Wylie, entre outros, sugeriram a construção gráfica de um diagrama fornecendo a distância entre o limite superior e inferior de cada parâmetro, a partir do qual se pode esperar uma soldadura aceitável. Na elaboração de tal diagrama foi tomada a formação de ondas como indicação da presença de boa soldadura. Isto não corresponde necessariamente à verdade, pois foram detectados em alguns casos o aparecimento de más soldaduras, com separação das interfaces, apesar da existência das referidas ondas, devido ao efeito das ondas de tensão, que ocorrem após as soldaduras. Este efeito tardio foi constatado por El Sobky e Bblazynski. Mantendo essa ideia e apoiado pela evidência experimental, a onda pode ser aceite como um critério razoável, porque conduz à determinação da amplitude entre parâmetros com a qual é possível a manipulação das condições e ,assim, a eliminação de efeitos secundários podendo também ser feita a coincidência das ondas de tensão com a região de colisão. Este método é conhecido por "janela de soldadura". Os parâmetros críticos usados para estabelecer uma janela de soldadura são:
a) o ângulo crítico de colisão para a formação do jacto, L
b) a velocidade no ponto de colisão, Vc,
c) a energia cinética e a pressão de impacto na região de colisão associadas à velocidade de impacto, Vp.
Estas quantidades podem ser representadas simultaneamente num sistema de coordenadas -Vc.
A figura 2.5 mostra esquematicamente a representação da colisão num sistema monometálico.
Fig. 2.5
Janela de soldabilidade.
A zona a tracejado representa a janela de soldadura. A linha aa´ representa o ângulo crítico, c, necessário para a formação do jacto. O conjunto dessas curvas é dado pela figura 2.5 que representa os resultados obtidos por Abrahamson, Cowan e Holtzman. A linha bb´ representa o limite superior da velocidade Vc estimada de 1.2 a 1.5 vezes a velocidade do som. É, contudo, experimentalmente evidente que ao aproximar do limite superior de Vc restringe a escolha de outros parâmetros dentro da janela de soldadura.
Os limites superiores e inferiores do angulo dinâmico foram experimentalmente determinados por Bahrani e Crossland entre outros. Um limite inferior entre 2º e 3º e um superior de 31º têm sido sugeridos. Os valores superiores e inferiores do ângulo inicial ,num sistema inclinado, têm sido determinados entre 18º e 3º, respectivamente, onde os limites do actual ângulo dinâmico, correspondente a esses valores, podem ser estimados usando qualquer um dos diagramas já discutidos anteriormente
(2.12)
e são os representados pelas linhas cc´ e dd´ na figura 2.5. Como limite inferior da velocidade de colisão, das análises de Cowan conhecemos a expressão que define a velocidade mínima de transição, acima da qual a interface ondulada é obtida. Com o fluxo do fluido, um valor para o número de Reynolds equivalente é dado por:
(2.13)
Onde as letras C,F e B correspondem à região de colisão do componente voador e dos componentes das bases, respectivamente, e a pirâmide do diamante de dureza, H, é tomada como medida de dureza. A transição ocorre para Rc=10.6 e isto define o valor mínimo de Vc indicado na linha ee´ na figura 2.5. O último factor a ser determinado é a velocidade Vp que é responsável pela pressão de impacto e pela energia de impacto. A pressão de impacto é dada por:
onde C é a grandeza da velocidade do som.
Como uma certa pressão mínima deve existir, deve também haver uma velocidade mínima, Vp. Isto foi determinado por Wittman e é dado por :
(2.14)
onde HEL é a energia elástica limite de Hugoniot ( onde K é módulo de compactação, G o esforço de corte, a tensão de cedência ), ou em alternativa:
(2.15)
onde é o último tensor das tensões.
Ambas as equações fornecem valores para Vp e Pi de acordo com os resultados experimentais de Wittman.
Uma vez que a pressão mínima influencia a qualidade da soldadura, esta dependerá da quantidade da energia cinética dissipada na região da colisão. Wylie sugere que energia de impacto deve estar relacionada com a energia de tensão total até ao nível de cedência dinâmica, isto é:
(2.16)
Onde Ei é a energia de impacto, E é o módulo de Young, D é a tensão dinâmica de cedência, é uma constante e t é a espessura da peça voadora. Esta aproximação aparenta ser razoável mas depende da disponibilidade de valores precisos definidos para a tensão dinâmica de cedência D. A linha ff´ pode ser calculada e representa o limite inferior de Vp da figura 2.5.
A condição para que a fusão ocorra pode ser usada como base para o cálculo do limite superior da energia de impacto e subsequentemente o valor Vp. O aquecimento adiabático leva ao enclausulamento de uma porção de jacto de energia, provocando a elevação da temperatura, a qual pode causar a fusão de um ou de ambos os componentes, seguida de um rápido arrefecimento. As propriedades termofísicas da mistura na interface e também a condutividade térmica da placa voadora e da base vão gerir este processo. A equação
(2.17)
é uma expressão para o valor máximo que Vp pode ter em termos de propriedades térmicas. N é uma constante, Tm é o ponto de fusão, K é a condutividade térmica, Ch é o calor específico, Vc é a velocidade no ponto de colisão e t a espessura da chapa voadora.
A equação dada acima é representada na figura 2.5 pela linha gg´. Ainda nesta figura, a área sombreada representa a distância entre parâmetros com os quais se pode obter uma qualidade de soldadura aceitável. Resultados experimentais confirmam, em geral, a veracidade dos argumentos acima citados.
Tabela 2.2
Parâmetros de soldadura para obter uma interface ondulada e contínua (vários autores)
No caso de soldaduras bimetálicas, a janela de soldadura deve ser estabelecida para cada material em particular e depois em sobreposição entre eles. Isto irá resultar numa área de intersecção com a qual representaremos a gama funcional entre parâmetros aplicáveis à combinação em causa.
A tabela 2.2 fornece informação acerca da soldadura para combinações momo, bi ou tri metálica.
Ondas da interface
Introdução
A deformação periódica das interfaces, usualmente designadas por ondas de interface, é talvez o aspecto da soldadura por explosão mais discutido.
A existência deste período de deformação da superfície não está confinada às interfaces na soldadura por explosão, mas efeitos extraordinariamente similares podem ser encontrados em superfícies sólidas sujeitas à acção erosiva de jactos líquidos a alta velocidade, como por exemplo nas bombas, nas pás das turbinas a vapor e, claro, na interface do ar com o mar. De facto, a formação de ondas na soldadura por explosão pode ser vista, dentro de certas circunstâncias de fluxo, como um caso particular de um fenómeno geral de formação de ondas interfaciais. A presença do jacto na região de colisão e o comportamento momentâneo do fluido sob altas pressões na região de colisão conduziram muitos investigadores a procurar a explicação e a caracterização dessas ondas em termos de um mecanismo de fluxo de uma ou de outra maneira.
Mecanismos de formação da onda
Têm sido sugeridos diferentes mecanismos referentes à formação das ondas, mas, examinando-os detalhadamente, estes são maioritariamente de natureza qualitativa ou semi-qualitativa; como tal não é possível aceder a um tratamento analítico.
Recentemente focou-se um novo ponto importante que diz respeito à existência de múltiplos tipos de ondas e, por conseguinte, a possibilidade de cada um dos mecanismos propostos ter a capacidade de descrever apenas um tipo de onda. Daí a necessidade de uma observação mais pormenorizada ao mecanismo dos fluidos na zona de colisão, de modo a estabelecer um mecanismo a partir do qual se possam explicar os diferentes tipos de ondas. A ilustração abaixo evidencia três tipos de ondas. A figura 2.6 a) mostra um alto grau de rotação sem sinal apreciável de fusão. Na figura 2.6 b) nota-se uma frente de onda sem vórtice atrás, numa multicamada formando um compósito de cobre- latão- fio de aço. Obviamente, estão presentes alterações na frente do vórtice e na crista da onda. Na figura 2.6 c) mostra-se uma interface múltipla na qual se incluem ondas com uma frente e vórtices na parte traseira, interfaces planas e vários graus de assimetria.
É agora apresentada uma breve revisão dos mecanismos existentes, seguida por uma análise dos mecanismos de fluxo na região de colisão. De acordo com as analogias usadas em cada caso, os mecanismos podem ser classificados em quatro grupos:
(a) mecanismo de indentação por jacto.
Abrahamson postulou que as ondas são formadas pela acção de indentação do jacto saliente na placa de base e pela libertação periódica da depressão formada à frente do ponto de colisão pelo material, removida através do mecanismo de indentação. Isto permite que o jacto saliente ultrapasse a depressão e o processo continue. Bahrani dá uma descrição mais detalhada de como as ondas se formam, mas atribuiu a indentação ao jacto reentrante e a formação de vórtices à assimilação do material removido pelo jacto.
Fig. 2.6
Tipos de ondas de soldadura, (a) rotação sem fusão apreciável, (b) onda grande só com a frente em vortex, (c) ondas em interfaces múltiplas.
(b) Enquanto que os mecanismos de indentação indicam que as ondas são formadas essencialmente na zona de colisão, a instabilidade dos mecanismos de fluxo sugerem que elas são criadas à frente do ponto de colisão, segundo Hunt, ou perto do ponto de colisão, como defende Robinson, como resultado da descontinuidade da velocidade ao longo da interface que envolve o jacto reentrante e o jacto saliente, respectivamente. O processo de formação da onda é tratado como uma instabilidade de Helmolz. No trabalho de Hunt é postulado que a descontinuidade é de forma afiada e o jacto reentrante é necessário para a formação da onda. Assume-se, também, que o jacto reentrante deve permanecer em contacto com a chapa e que o comportamento do fluido não se estende ao jacto saliente. Já Robinson mostra que o valor da tensão dentro do jacto saliente é suficientemente alto para justificar o comportamento de fluido e que o perfil de velocidade através da interface tem um ou dois pontos de inflexão. Estas suposições permitiram-lhe classificar a superfície de deformação como uma superficie de vorticidade constante e obteve uma onda com crista enrolada.
(c) Mecanismos de eliminação de vórtices.
Cowan e Holtzman, Kowalick e Hay e Onzava e Ishi, sugeriram que o ponto de estagnação actua como um obstáculo sólido desde que um estado fixo tenha sido estabelecido e que essas ondas conduzam a um mecanismo de eliminação de vórtices, iniciado no ponto de estagnação e continuando a crescer por trás da região de colisão. Em adição a estes mecanismos, fórmulas empíricas sugeridas por Deribas dão resultados na previsão do comprimento da onda. Isto é dado por:
(2.18)
Soldadura por explosão em geometrias planas
Dos vários componentes soldados por explosão agora disponíveis, as chapas revestidas têm uma produção mundial de cerca de 25000 m2 por ano, embora estas tenham uma larga aplicação directa, tal qual são produzidas, em formas planas mais simples como rectângulos ou discos, outras formas podem ser obtidas com facilidade a partir das chapas planas revestidas, usando técnicas de fabricação convenientes. Exemplos concretos disso são as extremidades esféricas dos permutadores de calor e dos vasos de pressão feitos de aço estrutural, interiormente revestidos de uma fina camada de material resistente à corrosão como o aço inox ou titânio. Para algumas aplicações uma só placa longa revestida pode ser maquinada para providenciar numerosas juntas de transição que podem ser planares ou tubulares.
O revestimento comercial envolve, por razões económicas, chapas e camadas de protecção de grande área e espessura constante e explosivos detonados subsonicamente que permitem a ocorrência de uma soldadura a uma distância constante entre a chapa voadora e a chapa a revestir. A última condição impõe a restrição de que a velocidade de revestimento ou a velocidade no ponto de colisão é neste caso igual à velocidade de detonação do explosivo, que pode não ser o ideal para a combinação de metais em causa. Para soldaduras de pequena escala, os componentes planares a serem unidos podem ser mutuamente inclinados e condições óptimas de ligação podem ser obtidas por uma ou mais técnicas de soldadura. Exemplos destas aplicações menores incluem técnicas de costura e ponto em folhas finas, o topo e a faixa a soldar das chapas e a soldadura de lâminas em camadas usando uma placa direccional. Finalmente, no trabalho de pesquisa e desenvolvimento da soldadura de novos materiais, o uso de geometrias planares pode ser um meio conveniente para estabelecer parâmetros, que podem ser aplicados a outras geometrias com ajuda de equações apropriadas.
Combinação de materiais e espessura da chapa voadora
As várias combinações de metais e as ligas metálicas unidas com sucesso pela soldadura por explosão remontam a 1964, foram divulgadas por Pocalyko e Williams of Du Pont e são apresentadas na figura 2.7.
Fig. 2.7
Tabela de combinações de metais unidos através de soldadura por explosão desde 1964.
Têm sido usadas com sucesso placas voadoras de aço inoxidável, com uma área até 15 m2 e até 25 mm de espessura,. De acordo com Linse, em 1967, eram já conhecidas 260 combinações possíveis. A tabela 2.3 dá informação actualizada acerca de materiais de revestimento e espessuras para revestimentos comerciais (sob licença de Du Pont) por Nobel`s Explosives Company (NEC), Escócia. Otto e Carpenter demonstraram o revestimento com sucesso de placas de aço com chumbo, de grande área, que pode tornar-se um processo comercial. Algumas combinações adicionais de soldadura com sucesso em experiências de pequena escala, pelos autores, incluem:
Alumínio a ligas de Al-Zn-Mg
Alumínio a ligas de aço “Maraging”
Cobalto a ligas de aço macio
Cobre a ligas de duralumínio
Cobre a ligas de níquel
Cobre a ligas de nióbio
Cobre a ligas de vanádio
Platina a ligas de titânio
Aço de Hadfield a ligas de aço ao carbono
“Armour plate” a ligas de aço ao carbono
Os factores que determinam a soldabilidade são a ductilidade, o ponto de fusão e/ou a gama de congelamento, a densidade e a espessura de um ou dos dois componentes. Du Pont e outros têm sugerido que uma elongação de pelo menos 5% no teste standard da tensão ou um mínimo de 14 J no ensaio de impacto Charpy, com entalhe em V, seja um requisito da chapa voadora ou do material de revestimento. Com isto pretende-se evitar a rotura durante o processo de revestimento e que um dos componentes do compósito desejado seja relativamente frágil. É uma prática normal para fazer deste último a base.
Assim, Wright, Bayce e Williams revestiram ferro fundido de grafite esferoidal e antimónio com aço macio. Richter, verificou que por vezes a chapa voadora comportava-se de modo mais dúctil que o alvo e também exibia menos elongamento.
Por exemplo, o ferro fundido de grafite esferoidal, não pode ser soldado com os parâmetros de explosão que usou, pois partia quando usado como chapa voadora. Este conflito aparente pode ser explicado por diferenças no nível e/ou duração da carga hidrostática da chapa voadora em diferentes investigações. Molibdénio TZM, que é demasiado frágil para ser soldado por resistência, pode ser soldado com sucesso por explosão.
Materiais de ponto de fusão muito baixo, como os fusíveis de bismuto – cádmio, fundem tão rapidamente durante o impacto que é difícil evitar a presença de fusão no tempo crítico quando as ondas de rarefacção atingem a interface temporariamente enfraquecida.
A soldadura torna-se mais difícil (a janela de soldadura torna-se mais pequena) quanto maior for a diferença das densidades entre os dois componentes e uma diferença de 9 g/cm3 tem sido sugerida como um valor limite. À medida que a diferença de densidade entre os componentes aumenta, também aumenta a perda de simetria e, embora a interface possa reter um padrão regular com formas repetidas, torna-se mais plana e mais material expulso pelo jacto tende a ser capturado, possivelmente por causa do componente menos denso, e como tal mais rápido. Usando uma camada intermédia de alumínio puro entre uma liga de alumínio e aço, pode ser alcançado uma ligação satisfatória. Isto por causa do ponto de fusão e condutividade térmica superiores, que reduzem tanto a quantidade de material fundido como o tempo no estado líquido para níveis nos quais em vez da interface alumínio/aço ser plana, formar ondulação. A interface Al/Al-Zn-Mg é sinosoidal por causa da semelhança de densidades e a fusão é isolada nas cristas e vagas das ondas bem desenvolvidas. São indicados na tabela 2.3 espessuras de chapa voadora de vários materiais.
Fig. 2.8
Na figura 2.8, imagem da esquerda é um exemplo da aplicação de uma camada intermédia de tálio para permitir a ligação de titânio com aço.
A imagem da direita, mostra regiões escuras de titânio, intensamente trabalhadas a frio, e aqui não há evidência de formações intermetálicas e as propriedades de ligação não foram praticamente afectadas.
Tabela 2.3
Vários materiais de revestimento e suas espessuras.
Selecção de parâmetros de ligação
Considerações gerais
Na soldadura por explosão duas considerações primárias são conhecidas:
(1)- A velocidade de impacto deve ser suficiente para gerar uma pressão de impacto de pelo menos 10 vezes a tensão de cedência do componente mais forte.
(2)- O ângulo de colisão deve exceder um valor mínimo para que, com a pressão de impacto disponível, permita a formação do jacto na superfície de cada material.
Estes, juntos, determinam a velocidade do ponto de colisão.
Fig. 2.9
Influência do substrato e da espessura do explosivo na velocidade de detonação.
É conhecido o aumento da velocidade de detonação com a espessura do explosivo, como se vê na figura 2.9.
Fig. 2.10
De seguida dão-se exemplos de aplicações da soldadura por explosão e várias ilustrações referentes ao tema.
Fig. 2.11
Exemplos de geometrias básicas usadas para produzir juntas de sobreposição entre barras rectangulares.
Fig. 2.12
Exemplos de geometrias de soldaduras lineares.
Fig. 2.13
Juntas topo a topo (esquema).
Fig. 2.14
Geometria básica de soldadura inclinada. As linhas a tracejado mostram posições de detonação e frentes de colisão, imediatamente após o início da soldadura.
Fig. 2.15
Exemplos de áreas não soldadas (sombreadas), associadas à carga de iniciação. (a) iniciação ao canto. (b) iniciação central.
Fig. 2.16
Geometria paralela. As linhas a tracejado mostram a posição das chapas voadoras quando a frente de detonação atinge a posição ilustrada.
Fig. 2.17
Esquema de soldadura e modo de colapso, utilizando uma chapa de impacto.
Fig. 2.18
Soldadura paralela (a) e inclinada (b), em geometrias tubulares.
Fig. 2.19
Técnica de ligação paralela de tubos. Cargas em anel (a-d), ou em esfera (e-h).
Fig. 2.20
Sistemas de soldadura por explosão e implosão. (a) Philipchuck, (b) Du Pont de Nemours, (c) por explosão, (d) por implosão e (e) por explosão e implosão (Blazynsky e Dara).
A deformação plástica manifesta por si só um aumento da tensão de cedência do material e mesmo quando relativamente pequeno afecta substancialmente as propriedades do conjunto, como se vê na figura 2.21
Fig. 2.21
Curvas tensão-defomação antes e depois da soldadura
Fig. 2.22
Variação morfologia da onda.
A figura 2.21 mostra bem como a morfologia da onda na interface da ligação (soldadura) varia com a velocidade de detonação.
Seguidamente mostram-se algumas imagens de aplicações práticas.
Outras considerações sobre a soldadura
As explosões para soldadura devem ser feitas numa mina, adaptada para o efeito, ou ao ar livre, distanciado pelo menos 7 Km de áreas residenciais por causa do ruído. Durante a explosão e num raio de 500 metros não deve haver pessoas, excepto os operadores.
Para minimizar o ruído, as explosões podem ser feitas em câmaras de vazio ou dentro de água.
Para o processo se tornar mais económico é comum empregar-se mais de 1 tonelada de explosivo por detonação.
A velocidade de detonação requerida é de 1500 m/s a 3000 m/s.
Entre os explosivos mais utilizados encontram-se: nitrato de amónio com fuel-óleo, pós com base em nitro-glicerina, TNT - nitrato de amónio e PETN - nitrato de amónio. São também utilizados perclorato de amónio, amatol e nitroguonidine1. Gelatinas e folhas explosivas não se empregam em larga escala.
O acabamento superficial dos metais a soldar requer um polimento de cerca 2,54m.
Podem-se empregar acabamentos inferiores, em detrimento da qualidade de soldadura.
Exige-se uma base em aço (o maior possível), excepto quando se faz revestimento nas duas faces ao mesmo tempo, ver fig. 2.16.
Há casos em que se exige um alívio de tensões, como, por exemplo, para o titânio, 1 hora a 625 ºC para 25 mm de espessura total.
O teste por ultra-sons é indicado para este tipo de soldadura (sondas de 10 a 25 mm de diâmetro, com frequências entre 2 e 5 MHz ).
A título de exemplo, a empresa Nobelclad aplicou, nos últimos 10 anos, 43 revestimentos de Ti e 4 de inox, em permutadores de calor de centrais térmicas.
BROCAS
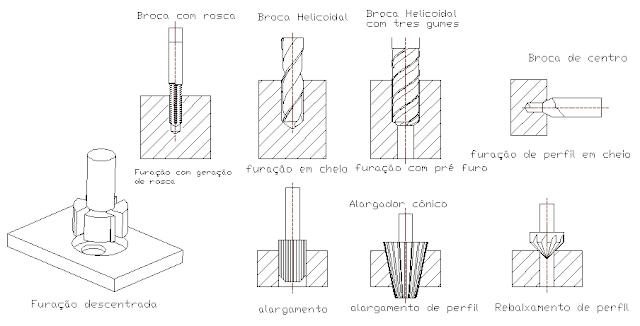
PROCESSO DE FURAÇÃO A furação é um dos processos de usinagem mais utilizados nas indústrias de manufatura. Tem por objetivo a obtenção de furos geralmente cilíndricos, podendo apresentar algumas variantes para o produto do processo (ver figura 2.8). A grande maioria das peças de qualquer tipo de indústria tem pelo menos um furo e, somente uma parte muito pequena dessas peças já vem com o furo pronto do processo de obtenção da peça bruta (fundição, forjamento, etc). Em geral, as peças têm que ser furadas em cheio ou terem seus furos aumentados através do processo de furação. (DINIZ et al, 2006). A furação faz parte do grupo de processos de usinagem com geometria de corte definida assim como o torneamento e o fresamento, envolvendo aproximadamente 30% de todas as operações de usinagem de metal e 75% do volume de material removido na usinagem (CASTILLO, 2005). Conforme a norma alemã DIN 8589, é definida como um processo de usinagem com movimento de corte circular, ou seja, com mov...
Comentários
Postar um comentário